Stress
The internal forces and moments generally vary from point to point. Obtaining this distribution is of primary importance in mechanics of materials. The total force in a cross-section, divided by the cross-sectional area, is the stress. We use stress to normalize forces with respect to the size of the geometry.Units
The units of stress can be found in the table below.
Table screenshot from ref pages

Table screenshot from ref pages
- Tension: \( \sigma > 0 \)
- Compression: \( \sigma < 0 \)
Stress under general loading conditions
We consider a homogeneous distribution of the internal force \( \Delta F \) over an infinitesimal area \( \Delta A \). The stress is defined by the infinitesimal force divided by the infinitesimal area.- Normal Stress: Defined by the intensity of the force acting NORMAL to \( \Delta A \)
- Shear Stress: Defined by the intensity of the force acting TANGENT to \( \Delta A \)
Average Normal Stress - Axial Loading
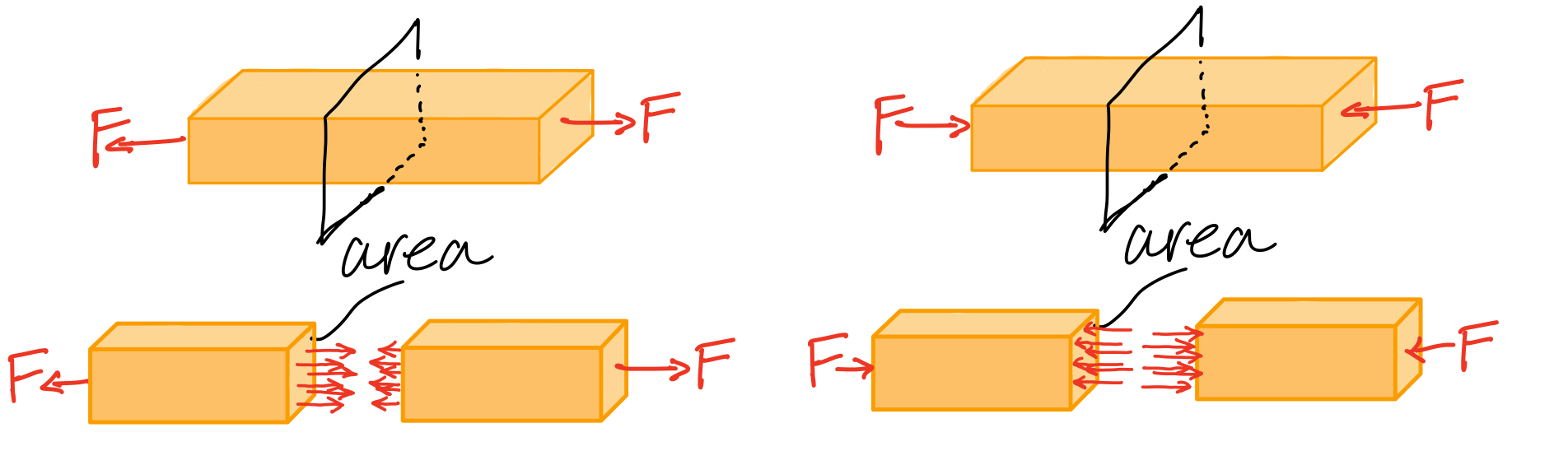
Normal stress
Average normal stress. #sts-ans
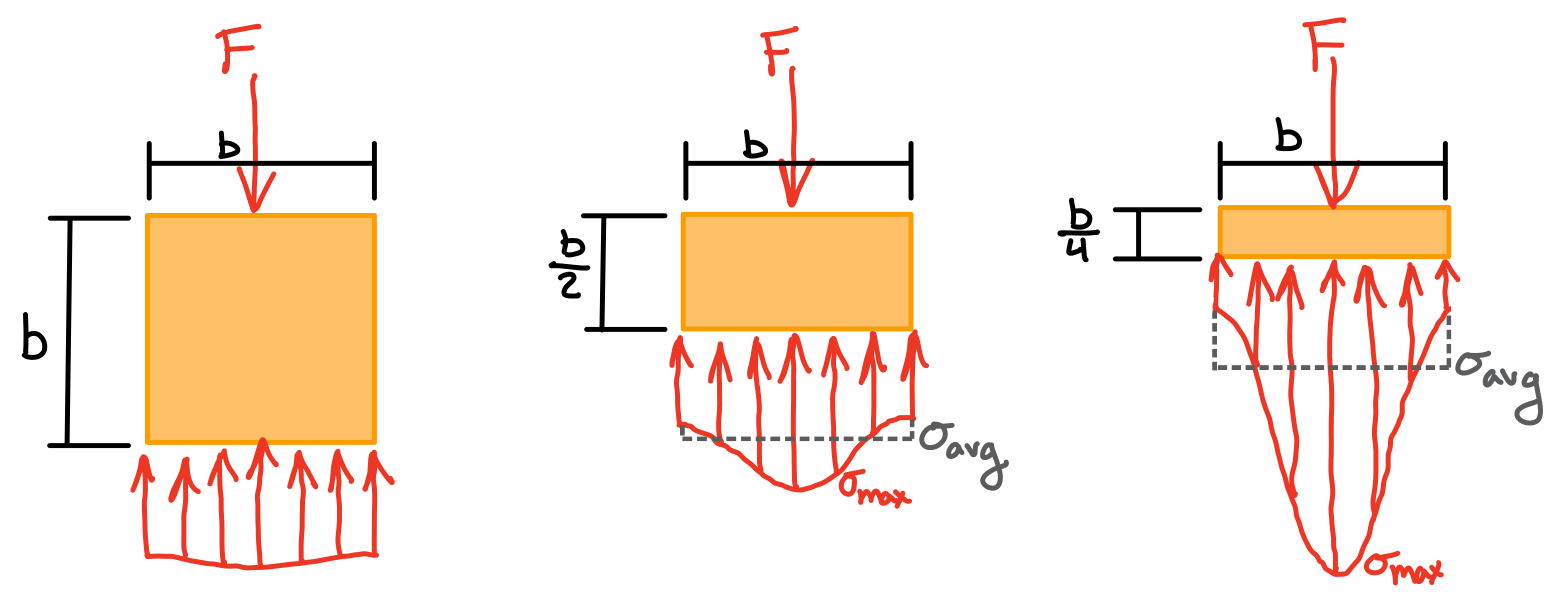
Non-uniform stress distribution
Average Shear Stress
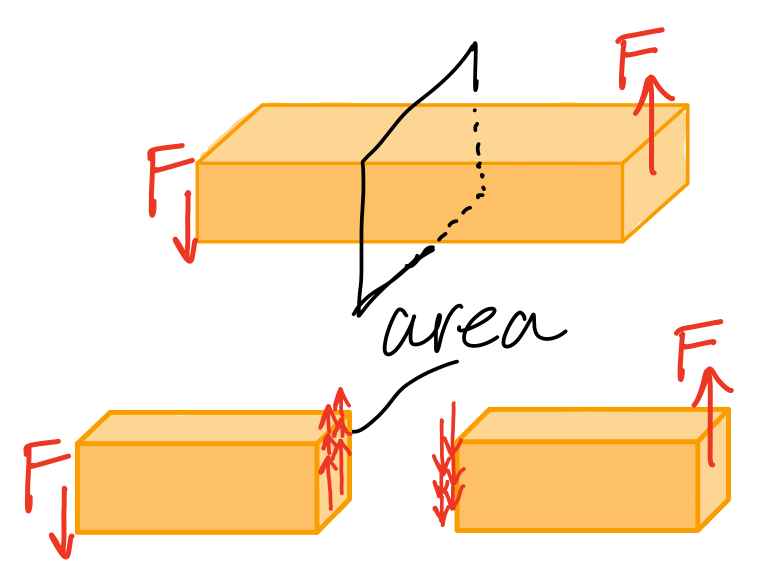
Shear stress
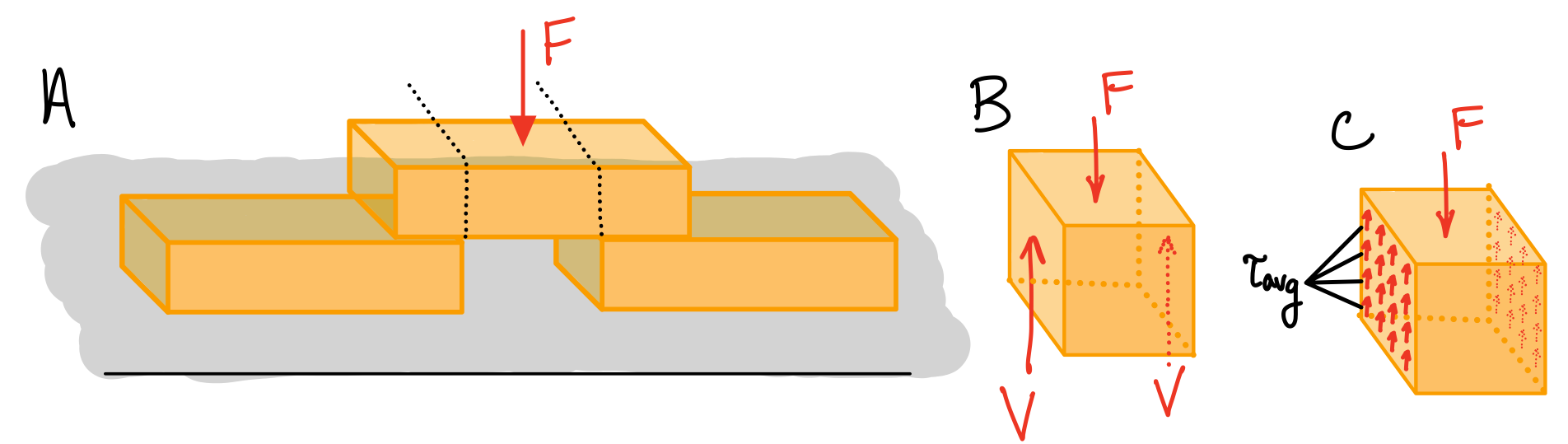
Average shear stress
Average shear stress. #sts-tav
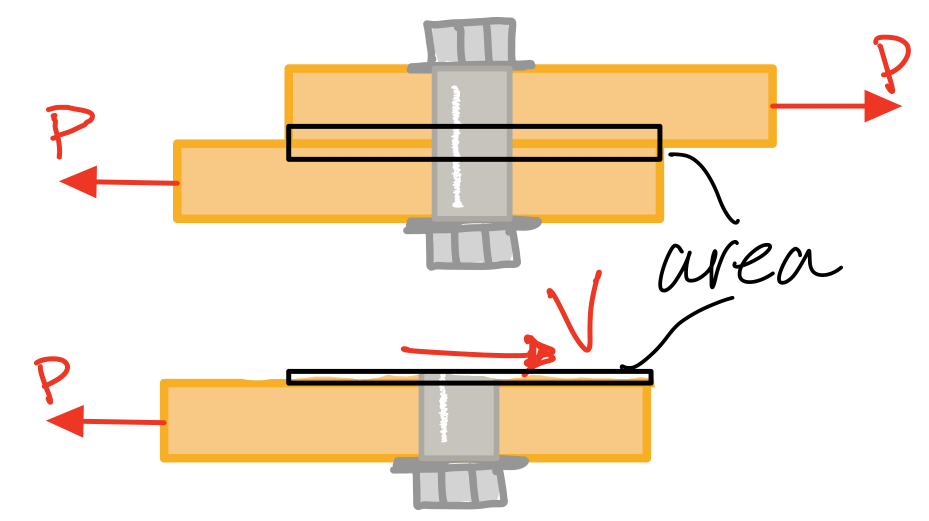
Single shear stress
Single shear stress. #sts-sss
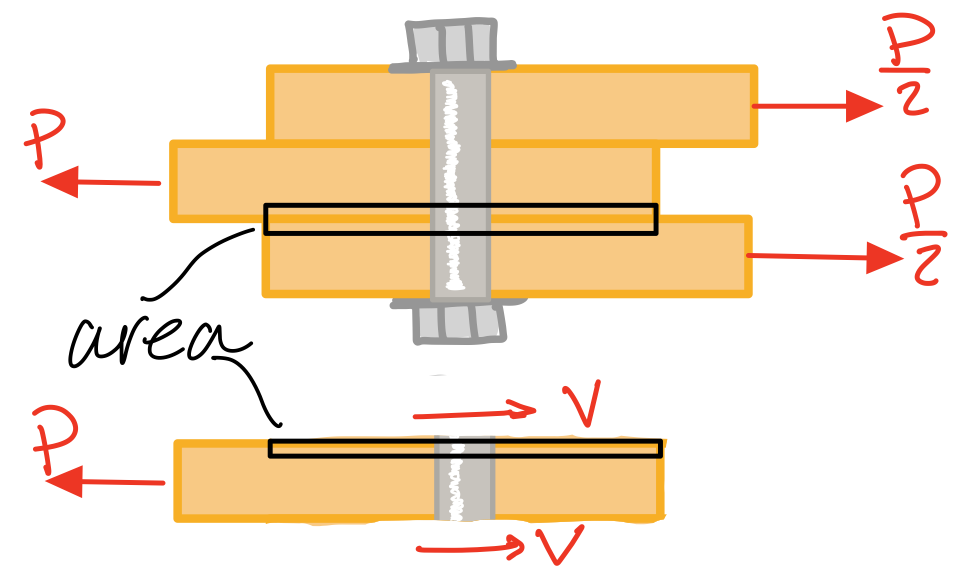
Double shear stress
Double shear stress. #sts-dss
Did you know?
Test content:
Did you know?
Test video:
Stress Tensor
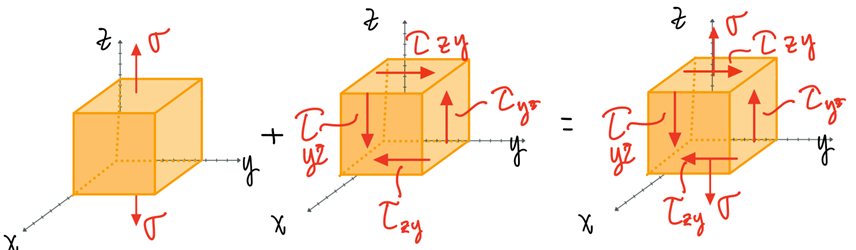
Stress element
- Three normal stress components: \( \sigma_x, \sigma_y, \sigma_z \)
- Six shear stress components: \( \tau_{xy} =\tau_{yx}, \tau_{xz}=\tau_{zx}, \tau_{yz}=\tau_{zy} \)
Support Reactions
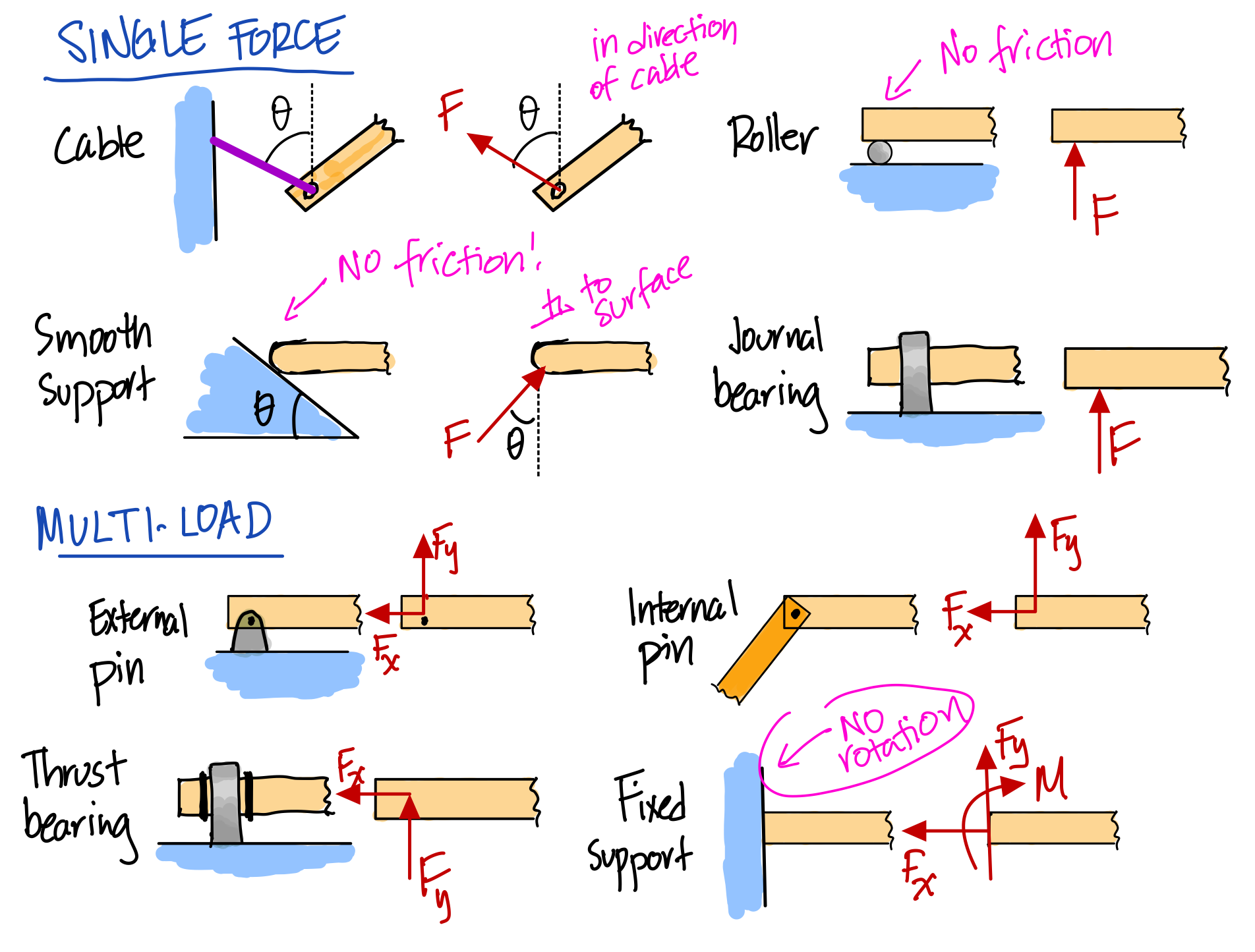
Support reactions
Allowable Strength Design
Design Requirement: A structural design is intended to support and/or transmit loads while maintaining safety and utility: don't break. Strength of a structure reflects its ability to resist failure.- Ultimate load ( \( P_u \) ): force when specimen fails (breaks).
- Ultimate normal stress ( \( \sigma_u \) ):